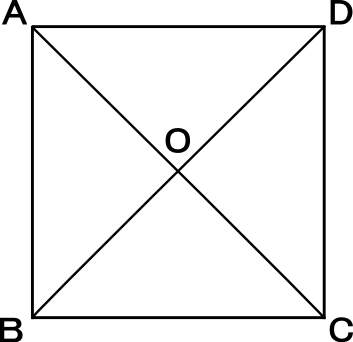
数学・算数 平行四辺形の対角線の交点を頂点とする三角形の面積 中1の数学の問題です。(回答解説をお願いします。) 図において、四角形abcdは平行四辺形で、acとbdの交点をoとし、辺ab上でae 質問no③ 平行四辺形の対角線は,それぞれ中点で交わるので,oa=oc,od=bd÷2 5 問題(3 学期) 次の平行四辺形abcd で,①~③の長さや角の大きさを求めよ。 ① ad ② ∠d ③ ∠c 解答欄 ① ② ③ 解答① 6cm ② 75° ③ 105° 解説 (1) 平行四辺形の向かい合う辺は等しいので,ad=bc (2) 平行四辺形の 「平行線の2本の対角線の交点は、互いに他の対角線を2等分する」、が正しい定理です。 ですから、OA = OC, OB = OD が成り立ちます。 特に、4つの角が90度のとき(長方形、正方形)、2本の対角線が等しいから、OA =OB = OC = OD となります。 0
数学図形において 平行四辺形の対角線の交点って 必ず各対角線 Yahoo 知恵袋
平行四辺形の対角線の交点
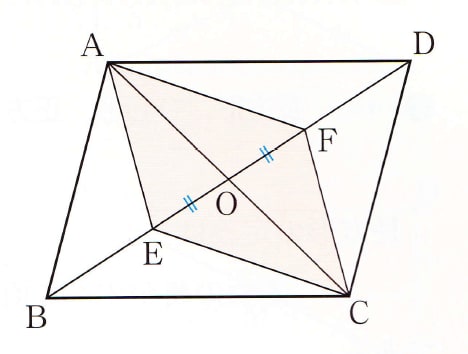
平行四辺形の対角線の交点-数学35章図形と相似「平行線と線分の比」<準備問題> 組 番 名前 1平行四辺形の定義を書きなさい。 2四角形が平行四辺形であるための条件が3つ書いてあります。あと2つ,条件を書きなさい。 ・2組の向かい合う辺がそれぞれ平行である。平行四辺形については,次のことも覚えておきたい。 • 平行四辺形のとなり合う内角の和は180 である。 • 平行四辺形は,対角線の交点を対称の中心とする点対称 な図形である。 • 平行四辺形の対角線の交点を通る直線は,その平行四辺 形の面積を2 等分する。 。(点対称の中心である対角



中2数学 平行四辺形の証明のポイントと練習問題 Examee
ブリタニカ国際大百科事典 小項目事典 平行四辺形の用語解説 2組の対辺がともに平行である四角形。次のような性質をもつ。(1) 2組の対辺の長さはそれぞれ等しい。(2) 2組の対角の大きさはそれぞれ等しい。(3) 2本の対角線はそれぞれの中点で交わる。1組の対辺が平行な四角形は台形なので平行四辺形は、対角線の交点を通る直線によって面積が2等分されるんでしたね。 長方形は平行四辺形の仲間なので、2つの対角線の頂点を通る直線を引くと、面積が2等分されます。 求め方は他にもあるので、チャレンジしてみてくださいね☆ 「面積が同じってことは重さも同じだよね!」と 平行四辺形は、点対称な図形である。対称の中心は、対角線の交点に等しい。 平行四辺形の対角線によって、平行四辺形を互いに合同な2つの三角形に分けることができる。 平行四辺形の面積sは 〔底辺〕×〔高さ〕 で求めることが
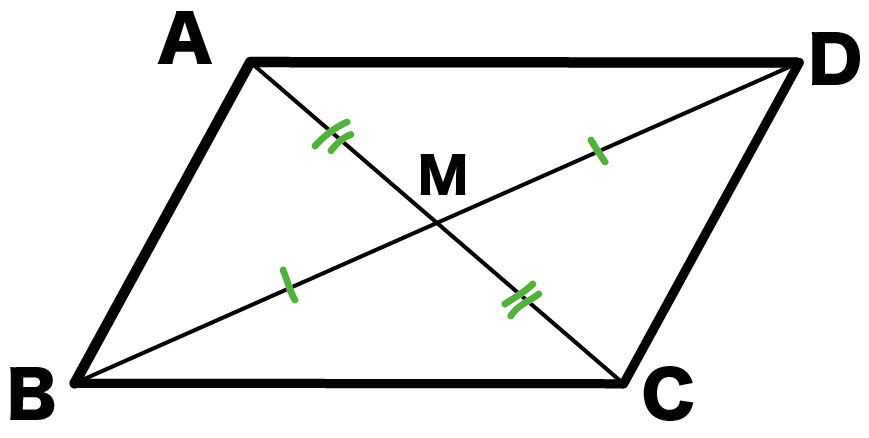
平行四辺形 abcd で対角線 bd をひくと も成り立ちます。さらに,対角線の交点を o とし,①の性質を利用すると ab = cd , ∠oab =∠ocd , ∠oba =∠odc より,ßoab ≡ßocd となり ③ oa = oc , ob = od も成り立ちます。 この方針をもとに,証明は各自で確認しておきましょう。 なお,四角形平行四辺形は、点対称な図形である。対称の中心は、対角線の交点に等しい。 平行四辺形の対角線によって、平行四辺形を互いに合同な2つの三角形に分けることができる。 平行四辺形の面積sは 〔底辺〕×〔高さ〕 で求めることが平行四辺形の対角線の交点oを通る直線をひき ac,bdの交点をp,qとする。このとき op=pqであることを証明 平行四辺形の証明 ズバリ解き方はこれ!|中学生/数学 中3数学中点連結定理ってどんな定理? まなビタミ 平行四辺形になるための条件 ①定義 2組の対辺がそれぞれ平行である。 ②
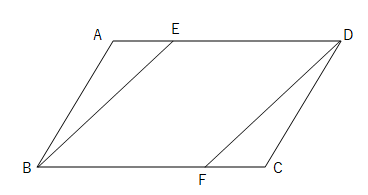
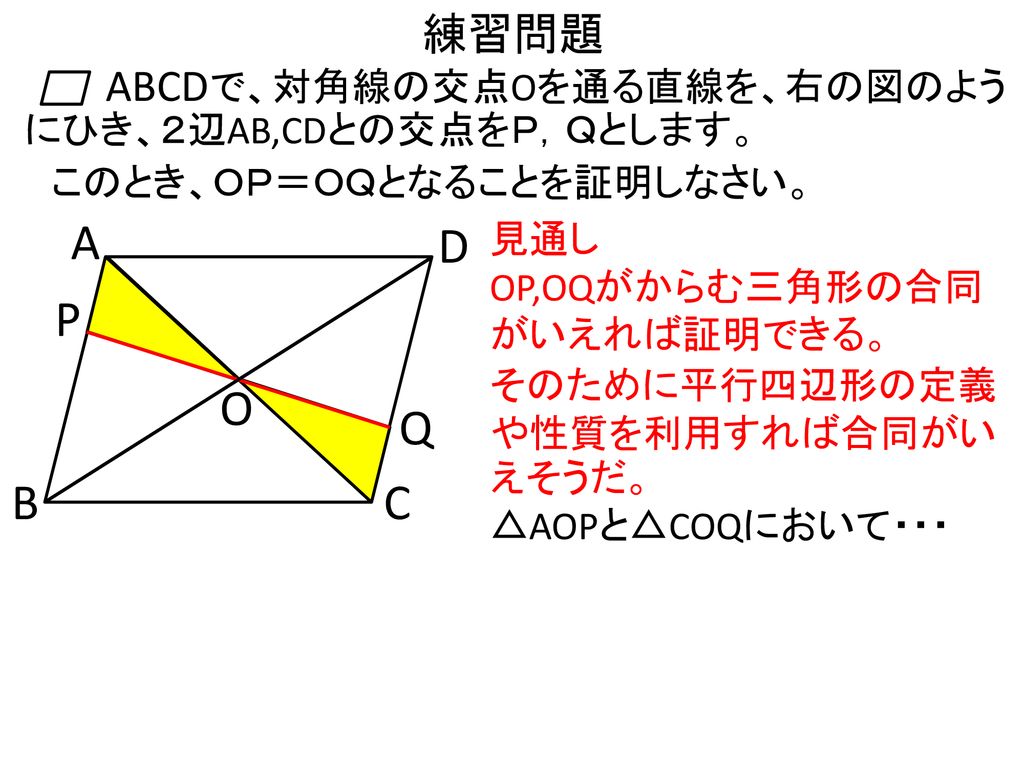
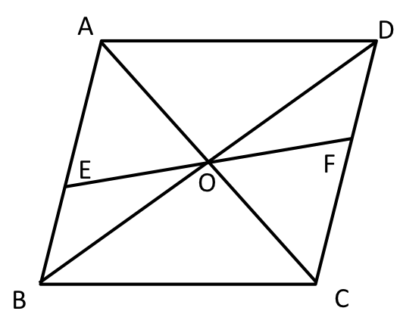
補助線で相似をつくる。 よく使う相似の形。 afの延長線とdcの延長線の交点をhとする。 するとab//cdから abf∽ hcfとなる。 bffc=21なので相似比は21である abとhcが対応する辺なので ab=4とするとhc=2となる。 また、ab//cdから aeg∽ hdgとなる。 ab=4ならcd=4なのでhd=6(3)2つの対角線がそれぞれAC=4cm,BD=6cmの平行四辺形ABCDを定規(ものさ し)を使って作図しなさい。 (4)1辺の長さが3cmのひし形ABCDを定規(ものさし)とコンパスを使って作図しなさい。 A B C A B C 数学25章図形の性質と証明「平行四辺形の性質」<基本問題①・解答> (1) ①BCに平行な線問3.平行四辺形abcd において,対角線の交点o を通る直線をひき,2辺ab,cd との 交点を,それぞれp,q とする。このとき,op,oq の長さの間には、どんな関係があり ますか。 op とoq が対応する線分となる 合同になりそうな三角形を探すと bop と doq と aop と coq の2つある。 どちらでも,お



中2数学 平行四辺形の証明のポイントと練習問題 Examee



中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく
③平行四辺形の対角線は abcdの対角線の交点o を通る直線が 辺ad tbcと交わる点をそれぞれ m t nとする このとき mo=noであることを証明 しなさい z証明 { aomと conにおいて 平行線の錯角は等しいからad//bcより ∠mao=∠nco・・・① 平行四辺形の対角線はそれぞれの中点で交わるから ao=co・ (ⅰ)対角線を1本引いて、2つの三角形について中点連結定理を使う。 (ⅱ)平行四辺形になるための条件のうち「1組の対辺が平行で長さが等しい」を使う。 このことをまず頭に入れておきましょう。 acとbdのどちらでもよいのですが、ここでは対角線acで考えます。 abcと adcのそれぞれ 平行四辺形の対角線の中点を通る直線は、どのように引いても、その平行四辺 pro0 137 136 もっと見る 80 pt 学習・教育 科学・統計資料 平行四辺形の対角線の中点を通る直線は、どのように引いても、その平行四辺形の面積を2等分しますか? これって中学数学?高校数学? 回答の条件 1人2回



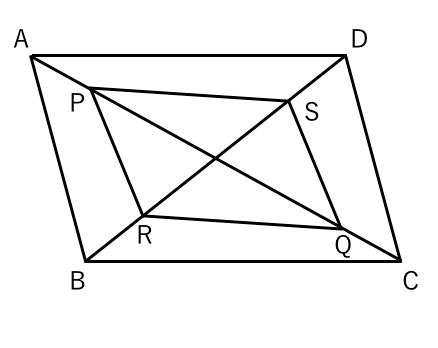
平行四辺形abcdで辺bcで中点をe 2本の対角線の交点p 対角線bdとaeの Yahoo 知恵袋



ラングレーの問題 整角四角形
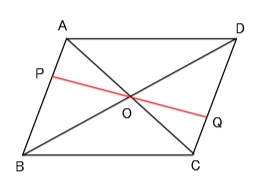
平行四辺形の定義 (AB//CD, AD//CB)から、「対角線はそれぞれの中点で交わる」を証明する。 A B C D O平行四辺形の対角線の交点はそれぞれの中点となるので、 bo=do・・・③ ①②③より1組の辺とその両端の∠が等しいので、 boq≡ dopである。 合同な図形の対応する辺の長さは等しいので、qb=pd。 中学校数学の目次 中学2年生 comment コメントをキャンセル メールアドレスが公開されることは また、平行四辺形の対角線の交点を求めたいのですが、求め方がわからなくて困っています。 それと、もうひとつ oabの面積を2等分する直線の式を求めなさい。 という問題があったのですが、これは三角形の中心を通る線を求めれば求まりますか? また



Www Tsumugi Ne Jp Member Data Sm2 5 Sm2 5 4 Pdf




3 Abcd0 e Descubre Como Resolverlo En Qanda
平行四辺形の対角線の交点を通る直線で,平行四辺形の面積は2等分されるんです! A B D C E a a b b A B D C E このページ掲載の文章・画像の無断転載平行四辺形は図1に示すように打1汀2打3汀4 とし,接点の一つとして例えば辺打1汀2上に Tlが指定されたものとする。 T4 図1 平成3年10月15日受理 中土木工学科助教授 2作 図法 作図法に関しては図1参照のこと。 21 準 備 対角線〃1〃3および汀2汀4をひき,その交点台形・平行四辺形・ひし形・対角線とは(1) 名前 台形 平行四辺形 ひし形 平行四辺形 長方形 ひし形 正方形 1次 の(1 )2 ようなせいし つ を持 四角形 、次 ア~オ 中からすべて選び記号 で答えなさい。



平行四辺形の面積の2等分



2
四角形ABCDで、 AB=CD、 ∠A=∠Cのとき、四角形は平行四辺形とは限らない。 四角形ABCD (対角線の交点をO)で、 ∠A=∠C、 AO=COのとき、四角形は平行四辺形とは限らない。形という. 性質10(平行四辺形の性質) (a) 平行四辺形の2 組の向かい合う辺は,それぞれ等しい. (b) 平行四辺形の2 組の向かい合う角は,それぞれ等しい. (c) 平行四辺形の対角線は,それぞれの中点で交わる. 性質11(平行四辺形になる条件) 四角形は,次すべての平行四辺形において 対角線をはさむ 二つの平行四辺形の補形は 互いに等しい。 平行四辺形は、定義の補足(命題1-34)による。 対角線は、定義の補足(命題1-34)による。 対角線をはさむ平行四辺形とは、 対角線の一端と対角線上の1点とを



中学2年数学練習問題 平行四辺形 長方形 ひし形 正方形 の性質




0 Oa Oc A D Descubre Como Resolverlo En Qanda
平行四辺形abcdの対角線の交点Oを通る直線が、ad、bcと交わる点をそれぞれm、nとするとき、四角形mbndは平行四辺形であること を証明せよ。 数学 プロ将棋棋士の一門って、どのくらいあるのでしょう。主なところは何でしょうか。 将棋、囲碁 平行四辺形の対角線の角度について こまた、平行四辺形の対角線の交点を求めたいのですが、求め方がわからなくて困っています。 それと、もうひとつ oabの面積を2等分する直線の式を求めなさい。 という問題があったのですが、これは三角形の中心を通る線を求めれば求まりますか? また、三角形の中心はa(2,2) b(2,2) d(0,0) 三点を平行四辺形は、点対称な図形である。対称の中心は、対角線の交点に等しい。 平行四辺形の対角線によって、平行四辺形を互いに合同な2つの三角形に分けることができる。 平行四辺形の面積sは 〔底辺〕×〔高さ〕 で求めることが
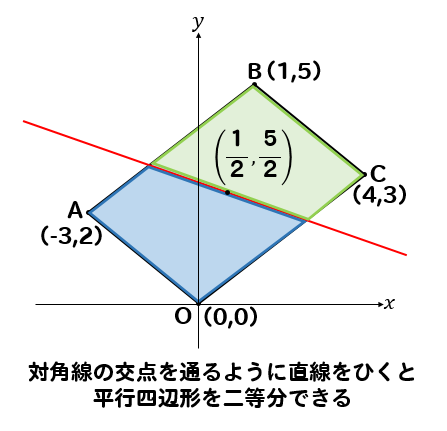



関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ



平行四辺形abcdがある 対角線の交点oを通る直線lをひき 辺ad Yahoo 知恵袋
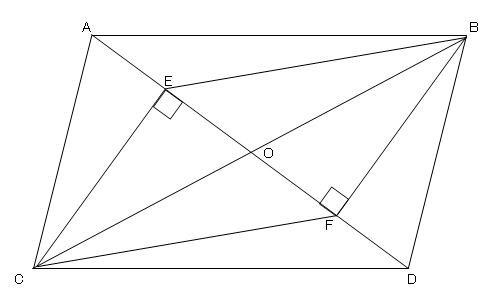
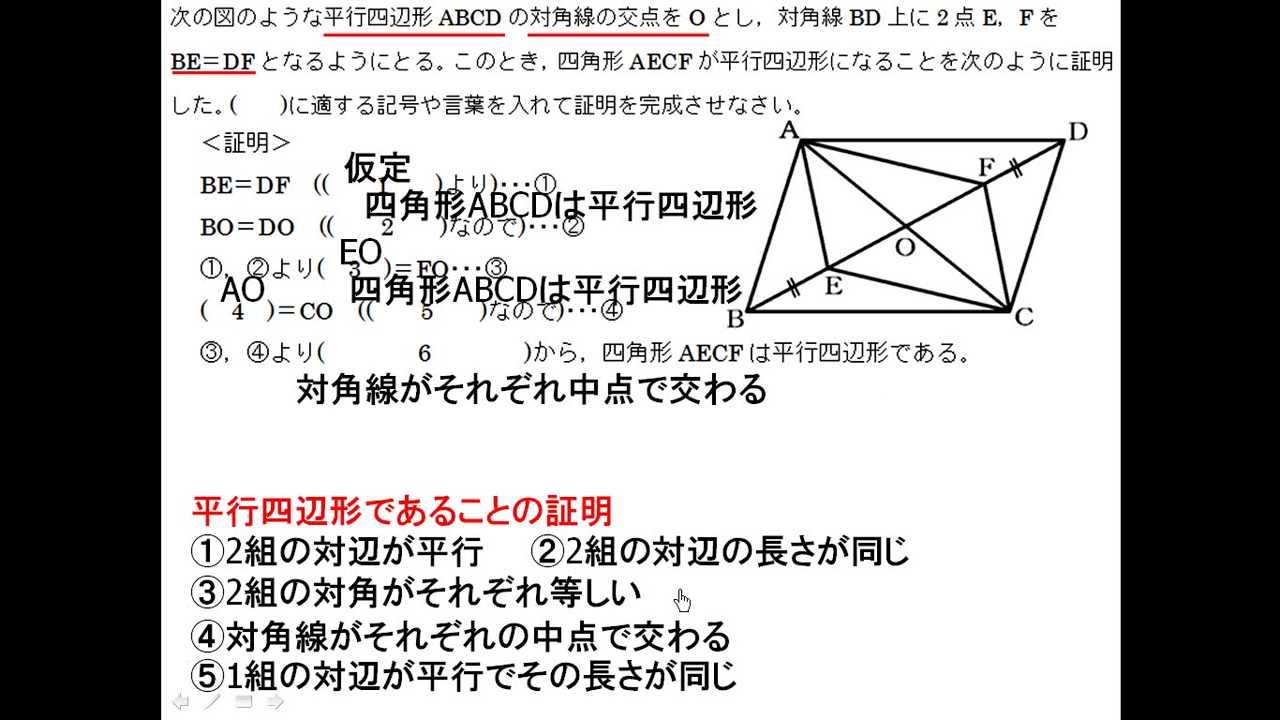
4頂点は、対角線の交点から等距離にある(円に内接する)。 平行四辺形の特別な形であるので、平行四辺形の性質を全て持つ。 等脚台形の特別な形であるので、等脚台形の性質を全て持つ。 菱形(斜方形、rhombus) 4辺の長さが全て等しい四角形。「平行四辺形の対角線はそれぞれの中点で交わる」ことを,次の ように証明しました。 証明 平行四辺形ABCDのAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators
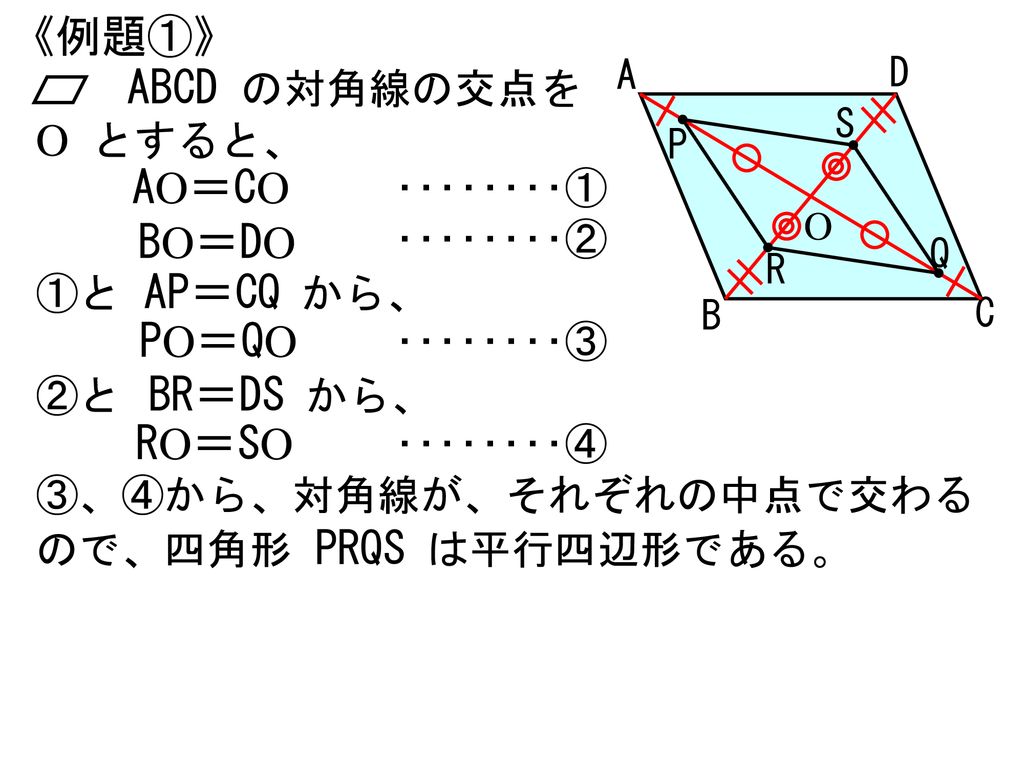



5 図形と合同 2章 平行四辺形 1 平行四辺形 5時間 Ppt Download
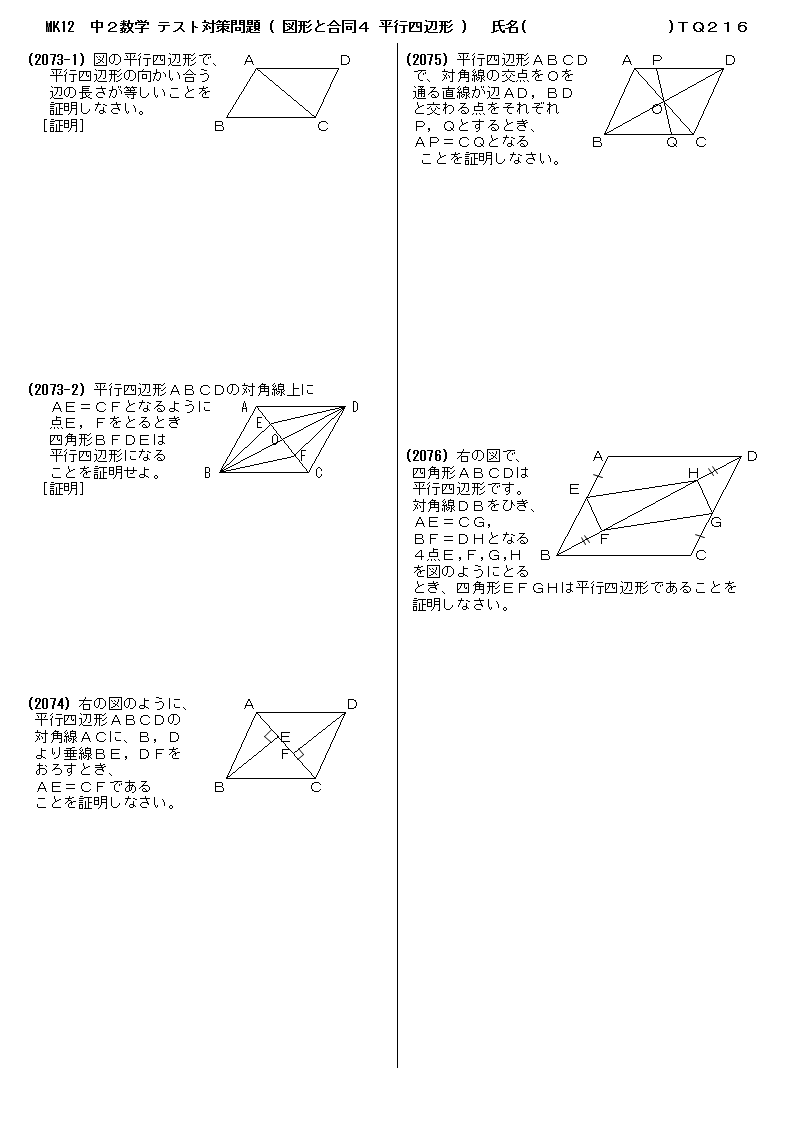



無料 中2数学 テスト対策 問題プリント 216 図形と合同4 平行四辺形
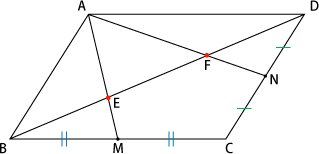
2年生 5 図形の性質と証明 知識・技能の習得を図る問題 年 組 号 氏名 全国学力・学習状況調査 A問題 ② 2 下のように「平行四辺形の2組の向かい合う辺はそれぞれ等しい」ことを証明しました。 Step2 平行四辺形の性質をつかう ひし形は平行四辺形だから、 平行四辺形の性質がつかえるね。 対角線は中点でそれぞれ交わる という性質より、 BM = DM・・・(2) Step3 三角形の合同条件をつかう AMは共通だから、 AM = AM・・・(3) (1)・(2)・(3)より、相似比の練習問題(平行四辺形5) 問1図のように、平行四辺形abcd の辺ad 上にae:ed =1:2 となる点e をとり、e から 辺ab に平行な直線を引き、辺bc との交点をf とします。さらに、対角線ac とef




中2数学 平行四辺形の証明のポイントと練習問題 Examee




平行四辺形の対角線の交点 点a Bは放物線y 1 2x 2上にあり 点cはx 数学 教えて Goo
一問ずつみていきましょう。 0:54 (1) A D B E を求めよ。 POINT:平行四辺形の対辺は等しい B E E C = 2 1 より、 A D B E = 3 2 (2) A Q Q F を求めよ。 図の対頂角、錯角の 2 組の角がそれぞれ等しいので、 A B Q ∽ F D Q POINT:相似な図形の対応する辺の比は




平行四辺形の対角線の交点を頂点とする三角形の面積 Okwave



対角線で参観 教育考現学
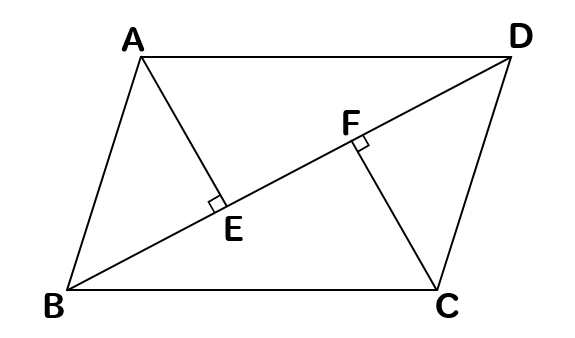



中学数学 平行四辺形の証明問題を徹底解説 数スタ



基礎学力アップシート 3年生 平行四辺形の辺の比を考えよう




平行四辺形のベクトルの問題です 番の解き方を教えて下さい Clear



Www Pref Osaka Lg Jp Attach Cyuu2goudou3kaku4kaku Pdf



平行四辺形を題材にした平面幾何の問題です F1 数学 箱根駅伝ブログ



証明 は と が Takapの数学日記
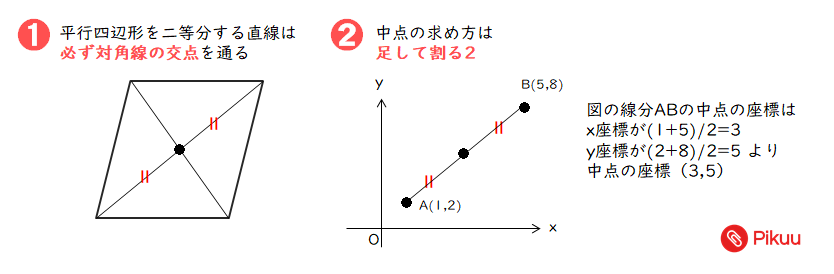



中学数学 平行四辺形の面積を二等分する直線を求める定期テスト予想問題 Pikuu




平行四辺形の問題です 1 4 までの問いの 解き方を教えてください M Clear



Www1 Iwate School Jp Action Common Download Main Upload Id 1332



ねらい 平行四辺形の定義と性質を理解し 定義から導かれた性質を 三角形の合同条件などを使って証明することができる Ppt Download




関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ




平行四辺形の定義と性質 証明問題の解き方 数学fun



平行四辺形の証明 4 ネット塾



Http Www Nier Go Jp Jugyourei H30 Data 18idea Mmath 03 Pdf




平行四辺形の対角線の交点の座標を求める はしもとの つれづれ



中2 数学 5 3 平行四辺形の証明 Youtube




四角形 Ict教材eboard イーボード




平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学




平行四辺形abcdの対角線の交点をoとして 対角線bdにoe ofとなる2 中学校 教えて Goo



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




無料 中2数学 テスト対策 解答プリント 216 図形と合同4 平行四辺形



1



ベクトルの問題です 平行四辺形oacbにおいて 対角線の Yahoo 知恵袋



1




平行四辺形の対角線の交点は どうやって求めるんですか 分かりづらい図ですみません Clear




Math 平行四辺形 平行四辺形になることの証明 働きアリ



フロー 2 5 5 2 平行四辺形の性質を利用した証明




平行四辺形の対角線が他の対角線の中点を通ることの証明 うさぎめし C



Http Www News Ed Jp Gimu Yumeako Gakuryoku H26 H26cyusu H26cyusua 7 Pdf




平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学
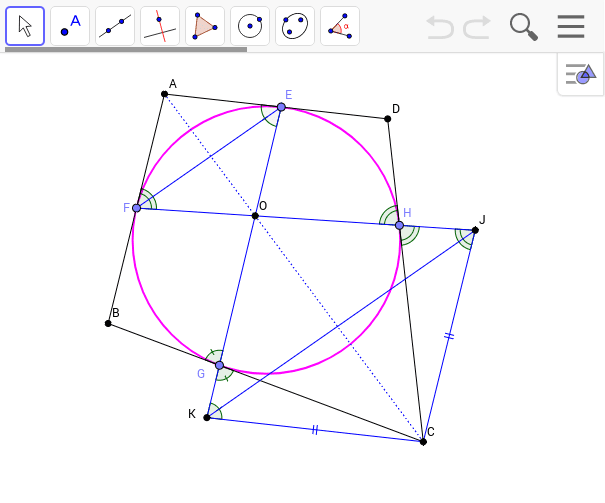



外接四角形の対角線の証明 Geogebra
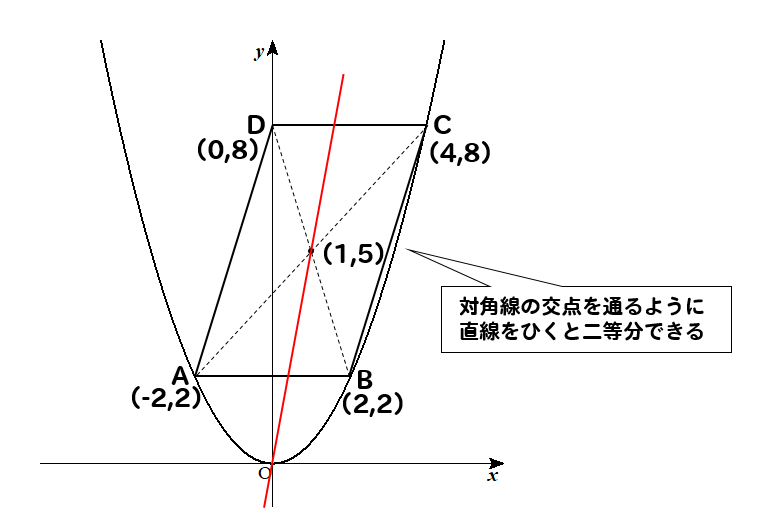



関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ



数学図形において 平行四辺形の対角線の交点って 必ず各対角線 Yahoo 知恵袋




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット
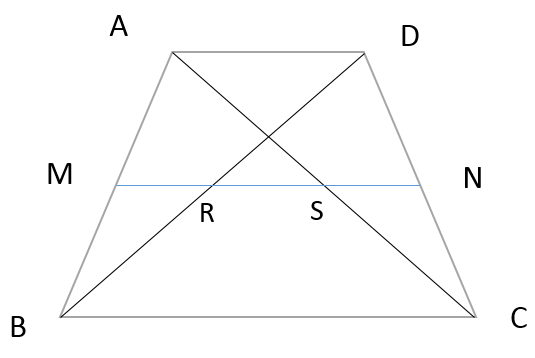



中学数学 中点連結定理 三角形 四角形 台形 偏差値40プログラマー



平行四辺形の対角線の交点は対角線を2等分にしますか 平行四辺形abcdと Yahoo 知恵袋



新しい数学2の問題なのですが四角形abcdの対角線の交点をoとしoa Oc O Yahoo 知恵袋




平行四辺形abcdの頂点a Cから対角線bdに垂線を引き 対角線との交点をそれぞれ Clear



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




平行四辺形 Wikipedia
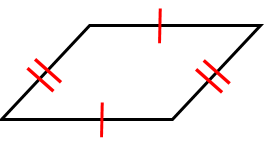



平行四辺形の3つの性質とその証明 具体例で学ぶ数学




数学 B 平行四辺形の頂点の座標 獨協医科大 大学入試数学の考え方と解法




高校数学b ベクトルの成分表示と平行四辺形 受験の月



1




標準 平行四辺形とベクトルの演算 なかけんの数学ノート




平行四辺形で知っておくべきこと 苦手な数学を簡単に




オイラー線の定理 Http Homepage2 Nifty Com Yoshio Oka Ma 人力検索はてな
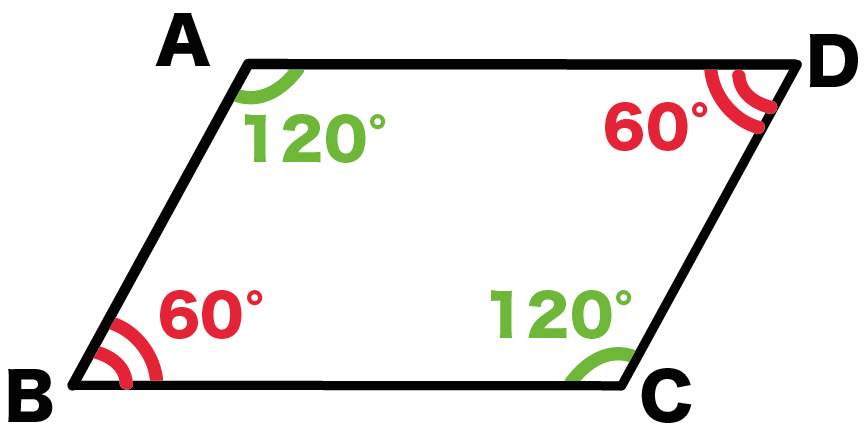



中2数学 平行四辺形の3つの性質 Qikeru 学びを楽しくわかりやすく



平行四辺形の面積の2等分




中学数学 平行四辺形の対角線 面積について 平行四辺形の対角 数学 教えて Goo



Mathematics 相似 5 中点連結定理と重心 働きアリ The 2nd



数学図形において 平行四辺形の対角線の交点って 必ず各対角線 Yahoo 知恵袋



平行四辺形に関する定理 雑学のソムリエ



今月の問題 平行四辺形




と を解説つきで教えてください Clear




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット




無料 中2数学 標準問題 解答プリント 232 平行四辺形3 長方形とひし形




高校数学 対角線の長さとなす角で表された四角形の面積公式 S 1 2pqsin8 裏技 の証明 対角線の長さの和が一定である四角形の面積の最大 受験の月



1




平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル




円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ




関数13 平行四辺形の面積の二等分 Youtube



Http Www News Ed Jp Gimu Yumeako Gakuryoku H24 H24cyusu H24cyusua 8 Pdf




4 Abcd 0 A D Descubre Como Resolverlo En Qanda
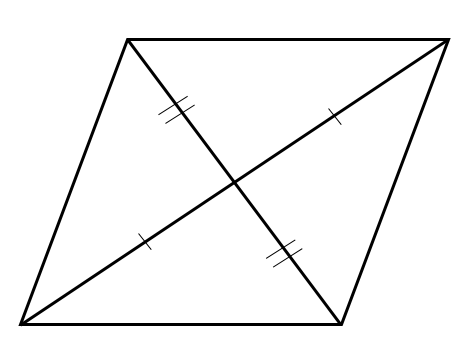



関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ




平面上のベクトル ベクトルの減法 Youtube
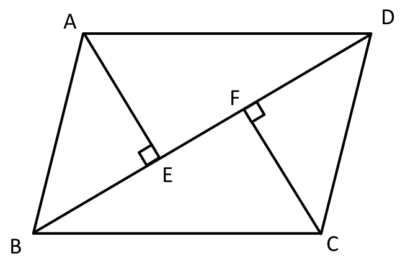



フロー 2 5 5 2 平行四辺形の性質を利用した証明
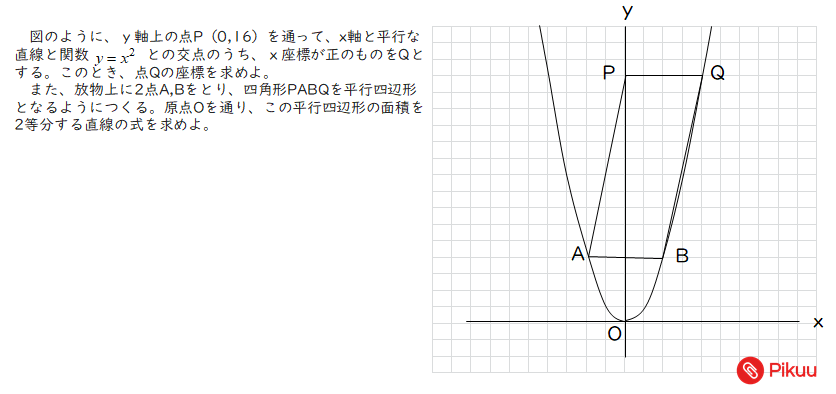



中学数学 平行四辺形の面積を二等分する直線を求める定期テスト予想問題 Pikuu



2



四角形に内接する楕円の作図 Geogebra
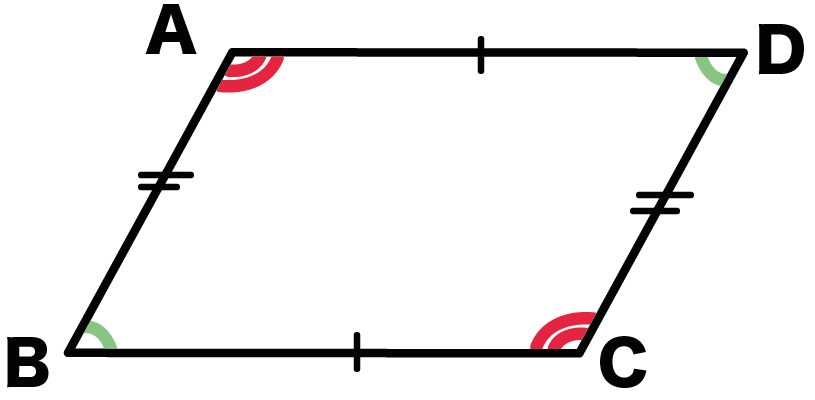



中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく
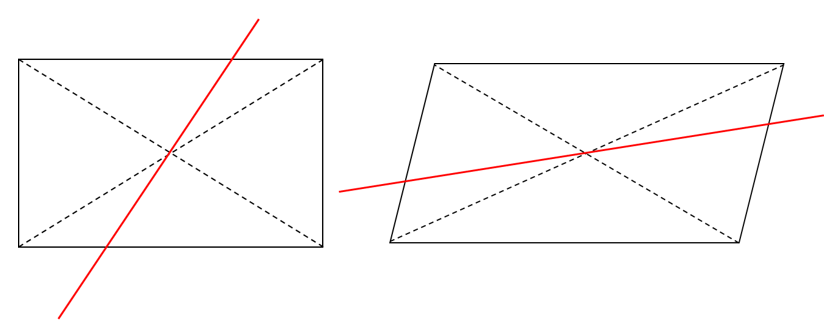



面積を2等分する考え方 中学受験プロ講師ブログ




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット
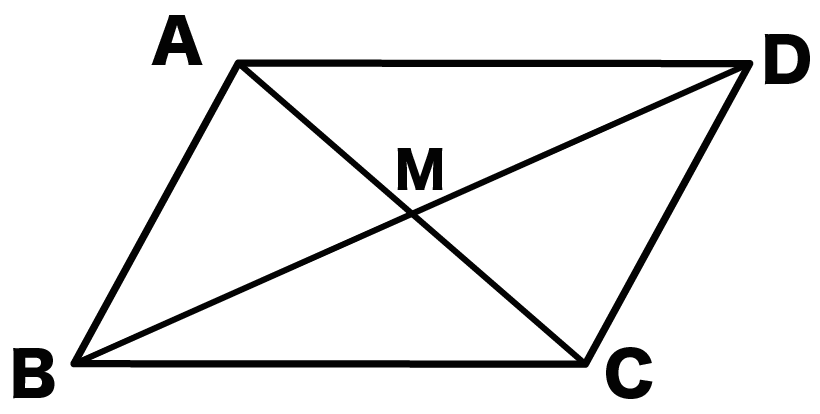



中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく
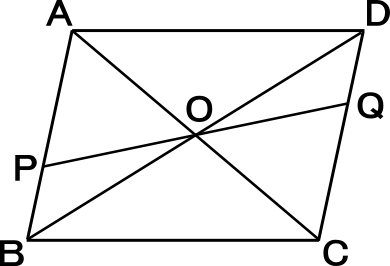



中学2年数学練習問題 図形と合同 平行四辺形の性質と証明問題
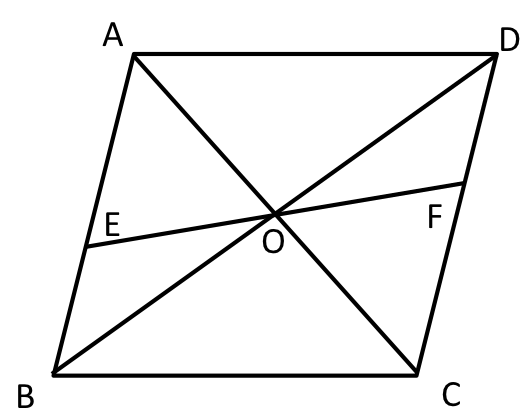



フロー 2 5 5 2 平行四辺形の性質を利用した証明




平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学
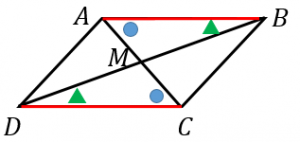



平行四辺形の3つの性質とその証明 具体例で学ぶ数学



いろいろな四角形 四角形の対角線 シリウス 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材




平行四辺形の座標 数学ii By Okボーイ マナペディア



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典
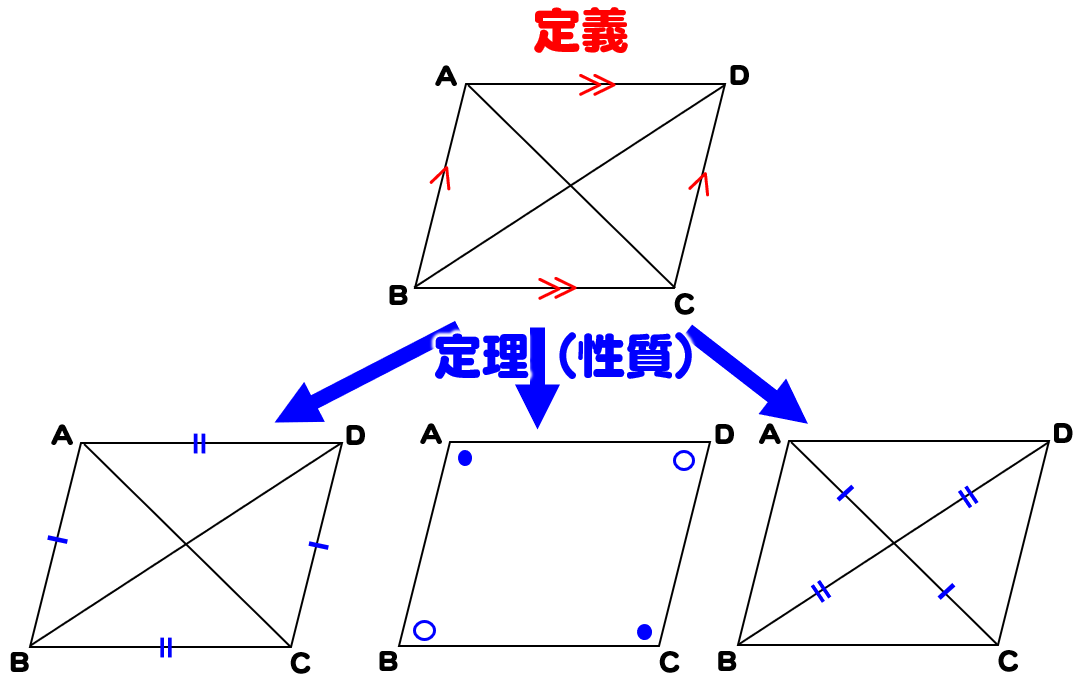



平行四辺形の定義と性質 証明問題の解き方 数学fun




平行四辺形の定義と性質 証明問題の解き方 数学fun



平行四辺形であることを証明する 苦手な数学を簡単に



中学2年数学練習問題 平行四辺形になる条件と証明方法 図形と合同



ラングレーの問題 整角四角形


